Proporção

A Proporção, a Arquitetura e a Matemática

Proporção é uma igualdade entre razões. De uma forma geral, dados quatro números reais e diferentes de zero (a, b, c e d), em certa ordem, se a razão entre os dois primeiros for igual à razão entre os dois últimos, ou seja, se a / b = c / d, podemos dizer que os números a, b, c e d, nesta ordem, formam uma proporção (FREITAS, 2008).

Na Arquitetura, a proporção é estudada desde a Antiguidade Clássica. É entendida como uma relação entre partes ou entre partes e o todo de uma edificação. Os arquitetos e engenheiros gregos e romanos primavam pelo belo e o harmônico e, para alcançarem seus objetivos, utilizavam a Proporção em seus projetos. Essa relação também pode ser encontrada em vários elementos da natureza. 

Segundo pesquisas arqueológicas, a proporcionalidade já era utilizada por povos pré-históricos que habitavam a região do Rio Danúbio, no leste da Sérvia. (SILVA, 2014). No sítio mesolítico de Lapensk Vir foram encontrados vestígios de edificações e constatado que possuíam medidas internas com proporções similares.

Vitrúvio, engenheiro e arquiteto romano da Antiguidade Clássica, descreveu, em seu importante Tratado de Arquitetura, De Architectura Libri Decem, estudos sobre Proporção no corpo humano. Ele percebeu que nosso corpo possui uma relação entre as partes e o todo, ou seja, as alturas de partes como cabeça, face, pé, mão, entre outros, se relacionam com a altura do corpo racionalmente. Um exemplo disso é a cabeça, que segundo ele, seria 1/8 da altura do corpo e a face 1/10 desse. O umbigo é o ponto central do corpo humano, uma vez que, colocando a ponta seca de um compasso sobre o umbigo de um homem deitado de costas com os pés e as mãos esticados e, formando um círculo a partir do dedo de alguma mão, os dedos das duas mãos e dos pés tocarão a circunferência formada (LIVIO, 2008) .

Na mesma Época, a proporção foi aplicada no Partenon, templo grego considerado patrimônio da humanidade. Segundo Ching (2002), os elementos que compõem a fachada desse edifício  se relacionam e ao analisarmos a razão entre as partes podemos encontrar a divina proporção. 

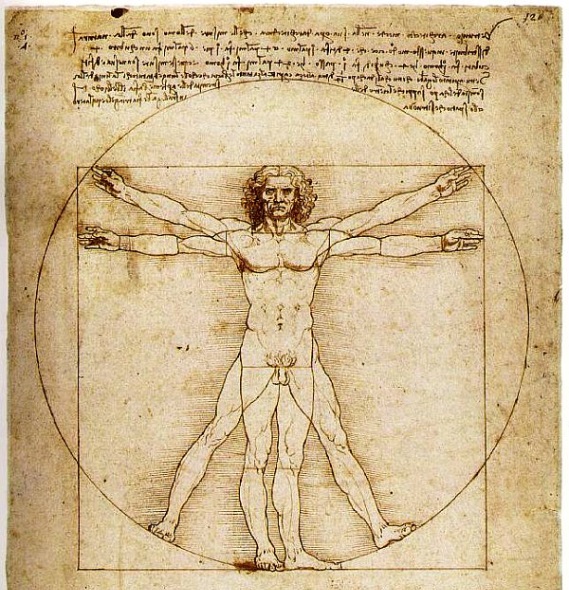
No Renascimento, as questões e os ideais da Antiguidade Clássica foram postos, novamente, em foco. Com isso, muitos artistas deste período foram influenciados pelos ideais e técnicas características da Antiguidade. Entre eles Leonardo da Vinci, que fez uma releitura do Homem Vitruviano, modificando algumas relações do corpo, como o pescoço, que seria 1 / 15 da altura do corpo ao invés de 1 / 24 e o pé que consistiria em 1 / 7 e não 1 / 6 daquele. 

Na Arquitetura Moderna, um arquiteto franco-suíço chamado Charles-Edouard Jeanneret-Gris, mais conhecido por Le Corbusier, destacou-se por valorizar a proporção em seus projetos. Ele elaborou um estudo sobre o corpo humano, "O Modulor", no qual o arquiteto aborda a proporção humana como uma escala universal. A partir desse estudo, que influenciou a arquitetura e a ergonomia, muitos objetos do dia a dia começaram a ser modificados para atender a escala humana. No caso dos edifícios que projetou, Le Corbusier relacionou a escala descrita em "O Modulor" e a divina proporção (SANTOS, 2007).

A Razão Áurea, também chamada de Proporção Áurea, Divina Proporção, dentre outros nomes, apresenta, segundo pesquisadores que a adotam, um aspecto estético agradável ao olhos. Convencionou-se identificá-la pela letra grega Φ (Phi maiúsculo), em homenagem ao escultor Phídias, responsável pelas esculturas do templo grego Partenon. Phi é o número irracional (1.61803398875...) obtido matematicamente através de sequências continuas infinitas, deduções algébricas ou geométricas (QUEIROZ, 2007).

Em termos científicos, essa relação foi citada, pela primeira vez, pelo matemático Euclides de Alexandria (300 a. C.),  em seu livro Elementos (SANTOS, 2007). Euclides apresenta a definição de Razão Áurea, inicialmente, relacionada a áreas. Posteriormente ele propõe a divisão de um segmento em média e extrema razão, cuja divisão do maior segmento pelo menor resulta na Divina proporção (LIVIO, 2008).

A seguir, a definição utilizada por Euclides (300 a. C.): "Diz-se que uma linha reta é cortada na razão extrema e média quando assim como a linha toda está para o maior segmento, o maior segmento está para o menor".

Divisão Gráfica do segmento AB em média e extrema razão:
Traçamos a mediatriz a fim de determinar o ponto médio M do segmento AB. Denominamos a medida do segmento AB de X. Desenhamos uma perpendicular ao segmento AB, a partir do ponto B, cuja dimensão é metade da medida do segmento AB (x/2). Desenhamos o segmento de reta AD. Utilizando um compasso, posicionamos a ponta seca em D, levamos a outra ponta até Be, por meio da interseção do arco com o segmento AD, determinamos o ponto E. Com a ponta seca do compasso em A, levamos a outra ponta até  E e determinamos o ponto C.

A razão áurea tem sido motivo de atenção por surgir em elementos da natureza, da Arquitetura, onde menos se espera. Um exemplo é a maçã, ao cortá-la pela circunferência, encontraremos as sementes dispostas em uma forma de estrela de cinco pontas, também conhecida como pentagrama. Cada um dos cinco triângulos isósceles que formam as pontas do pentagrama tem a propriedade de que a razão entre o comprimento do seu lado maior (L1) e o do lado menor (L2) é igual à Razão Áurea (aproximadamente 1,6180339887...), ou seja, L1/L2 1,6180339887...

O pentagrama está intrinsicamente relacionado ao pentágono. Em qualquer figura regular plana (lados e ângulos internos iguais) conhecidas como polígonos regulares, a soma de todos os ângulos internos é dada por 180. (n-2), sendo n igual ao número de lados do polígono. Por exemplo: O pentágono: 180. (5-2) = 540º, então cada ângulo do pentágono regular é 108º.

A razão entre a diagonal e o lado de um pentágono regular é igual à razão áurea. Traçando duas diagonais do pentágono encontramos um ângulo de 72 graus no triângulo formado pelas diagonais e o lado do pentágono. Traçando a bissetriz desse ângulo dividimos uma das diagonais do pentágono em proporção áurea.

Traçando as demais diagonais do pentágono regular obtêm-se o pentagrama. O pentagrama é uma figura plana que tem cinco lados e ângulos iguais. As diagonais também formam um pentágono menor no centro, traçando novas diagonais nesse pentágono central forma-se um novo pentagrama e um pentágono ainda menor (LÍVIO, 2008). Segundo Lívio (2008) essa progressão pode ser infinita, surgindo pentágonos e pentagramas cada vez menores.

No âmbito da Matemática, o número de ouro pode ser encontrado tanto na geometria quanto na aritmética. Nesse sentido, Fibonacci foi um pesquisador que se interessou pelo número de ouro. Ele usava, conscientemente, tal razão para a resolução de problemas matemáticos. Sua grande contribuição se deu por conta da resolução de um problema a respeito da procriação de coelhos, presente em seu livro, Liber Abaci. Na resolução, o autor obteve a sequência: 1, 1, 2, 3, 5, 8, 13, 21,... Pode-se perceber, analisando a sequência, que um termo, a partir do terceiro, pode ser obtido a partir da soma dos seus dois antecessores.

A sequência de Fibonacci, no entanto, não é conhecida apenas pela relação entre seus termos. Segundo Lívio (2008), a sequência de Fibonacci está longe de ficar limitada à reprodução de coelhos. Esta está ligada a diversos fenômenos naturais e não naturais. Entre esses estão: a reflexão da luz através de duas placas de vidro, a árvore genealógica de um zangão, a disposição de folhas ao redor do galho de alguma planta e o arranjo dos flósculos nos girassóis. A sequência Fibonacci também pode ser relacionada às seguintes estruturas:

Um conjunto de retângulos áureos pode ser gerado a partir de um retângulo áureo inicial qualquer, do qual é retirado um quadrado. Sobrará, dentro do retângulo, um novo retângulo menor, no qual os lados se diferem dos do primeiro por um fator de Phi. Esse processo pode ser realizado infinitamente e sempre resultará em um retângulo áureo menor que o que o gerou e diferente desse por um fator de Phi. 

Os Triângulos áureos são obtidos a partir de pentágonos, tais triângulos possuem a sequência de ângulos 36º-72°-72°. A razão entre alguns de seus lados resulta na Razão Áurea. Além disso, ao traçar a bissetriz em algum dos ângulos de 72° é gerado um novo triângulo áureo, a bissetriz também se encontra com o outro lado do triângulo inicial, dividindo-o, exatamente, na média e extrema razão.

Outra estrutura, na qual a razão áurea está presente, é a espiral logarítmica. Espiral que possui formato constante de acordo com o aumento do tamanho. Também é encontrada na natureza, como, por exemplo, nos chifres de um carneiro, em algumas galáxias e na curva das presas de um elefante. Também é comum em alguns tipos de moluscos, que produzem câmaras cada vez maiores, proporcionais ao seu crescimento. A espiral logarítmica pode ser obtida através de um conjunto de retângulos ou de triângulos áureos consecutivos. (LIVIO, 2008).

A razão áurea, retângulos áureos e espiral apresentada podem ser relacionados à sequência Fibonacci. Leonardo Fibonacci, matemático italiano, desenvolveu uma sequência de números 1,1,2,3,5,8,13,21,34,55,89, cuja a razão entre dois números inteiros consecutivos (Fn/Fn+1) a medida em que se avança na sequência tende a 1,6180339887..., a proporção áurea. Cada termo (começando com o terceiro) é igual à soma dos dois anteriores (LÍVIO, 2008).

Observação: Parte de Artigo elaborado pelo GPDTEC e publicado nos anais do Encontro Nacional de Educação Matemática 2016.

Bibliografia:

CHING, Francis D. K. Arquitetura, forma, espaço e ordem. São Paulo: Martins Fontes, 1999. 

FREITAS, Elizabete Alves de. Razão, proporção e grandezas proporcionais. Disponível em:. Acesso em: 16 mar. 2016. QUEIROZ, Rosa Maria. Razão Áurea: a beleza de uma razão surpreendente. Londrina, 2008. Disponível em: . Acesso em: 17 mar. 2016. 

LÍVIO, Mario. Razão Áurea: a história de Fi, um número surpreendente. Trad. Marco Shinobu, Rio de Janeiro: Record, 2008. SANTOS, Marcia. A Matemática da Arquitetura Ideal. In Graphica. Curitiba, 2007. Disponível em: . Acesso em: 17 mar. 2016. 

SILVA, Circe Mary. Onde está a proporcionalidade? Revista História da matemática para professores. Ano 1, nº1, março 2014.